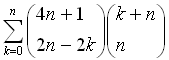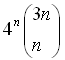Demonstration of the
On-Line Encyclopedia of Integer Sequences® (OEIS®)
(Page 8)

A Binomial Coefficient Sum
When analyzing the number of steps that a certain algorithm takes
to run, you encounter a binomial coefficent sum, perhaps:
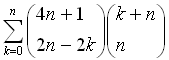
You know that there are
powerful methods available for automatically simplifying such sums
(see for example the book by M. Petkovsek, H. S. Wilf and D. Zeilberger,
A=B, Peters, Wellesley, MA, 1996;
or
Doron Zeilberger's web site).
But you are in a hurry, so you start by evaluating the
sum for the first few values of n. This produces the sequence
1, 12, 240, 5376, 126720, 3075072, ...
which you can then look up in the
OEIS.
One of three things will happen!
-
If you are very lucky, the sequence will be there, together with
a note that this is a binomial coefficent sum.
-
If you are just lucky, the sequence will be there
(but without a comment about it being a
binomial coefficient sum), in which case
you now have a conjectured binomial coefficent
identity that you can prove at your leisure by the
above-mentioned methods.
(You may also use the
Contributing a new sequence or comment
web page to send a comment
to the database.)
-
If the sequence is not there, you can use the same web page to
send the sequence, the summmation,
and anything else you know about it to the database.
This way the next person who encounters it
will be helped, and your name will
be preserved in the database!
In this particular example you were very lucky.
Here is the reply from the database.

|
|
|
| A006588 |
|
4^n*(3*n)!/((2*n)!*n!). |
|
+0
1
|
|
| 1, 12, 240, 5376, 126720, 3075072, 76038144, 1905131520, 48199827456, 1228623052800, 31504481648640, 811751838842880, 20999667135283200, 545086744471535616, 14189559697354260480, 370298578584748425216
(list)
|
|
|
OFFSET
|
0,2
|
|
|
REFERENCES
|
W. A. Whitworth, DCC Exercises in Choice and Chance, Stechert, NY, 1945, p. 35.
The right-hand side of a binomial coefficient identity in H. W. Gould, Combinatorial Identities, Morgantown, 1972; Eq. 3.115, page 35.
|
|
FORMULA
|
Sum_{k=0..n} binomial(4n+1,2n-2k)*binomial(n+k,k) = 4^n*binomial(3n,n).
a(n) ~ 1/2*3^(1/2)*pi^(-1/2)*n^(-1/2)*3^(3*n)*{1 - 7/72*n^-1 + ...} - Joe Keane (jgk(AT)jgk.org), Jun 11 2002
|
|
MAPLE
|
A006588 := n->add( binomial(4*n+1, 2*n-2*k)*binomial(n+k, k), k=0..n);
|
|
CROSSREFS
|
Sequence in context: A009052 A012303 A012538 this_sequence A009150 A009080 A002166
Adjacent sequences: A006585 A006586 A006587 this_sequence A006589 A006590 A006591
|
|
KEYWORD
|
nonn,easy,nice
|
|
AUTHOR
|
N. J. A. Sloane (njas(AT)research.att.com)
|
|
|

Thus your sum turns out to be equal to
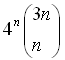
That particular sum is just one chosen at random from Gould's table.
The database contains sequences produced by many similar summations.
It would be nice to get more examples, particularly of sums where the answers
are rational numbers rather than integers. This would be an excellent
project for a volunteer.

Click the single right arrow to go to the next demonstration page,
or the single left arrow to return to the previous page.