Triple-Free Sets of Integers

Steven Finch, 9/5/2002

A set S of positive integers is called double-free if, for any integer x, the set . Equivalently, S is double-free if implies .

Consider the function



that is, the maximum cardinality of double-free sets with no element exceeding n. It is not difficult to prove that



in words, the asymptotic maximal density of double-free sets is 2/3. Here are details of the proof. Wang [1] obtained both recursive and closed-form expressions for r(n) and, moreover, demonstrated that



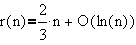
as n approaches infinity.

Let us now discuss a much harder problem. Define a set S of positive integers to be

• weakly triple-free (or triple-free) if, for any integer x, the set

• strongly triple-free if implies and .

Unlike the double-free case, the weak and strong senses of triple-free do not coincide.

Consider the functions





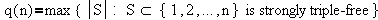
The second of these, q(n), has not attracted as much attention as the first. Eppstein pointed out to me in spring, 1996 that evaluating q(n) can be rephrased as finding the independence numbers of certain grid graphs. From here, Zimmermann computed an estimate of the strongly triple-free set constant:



Here are more details. Zimmermann's computation was based on a theorem proved by Cassaigne, and they subsequently prepared a joint report [2].

Graham, Spencer & Witsenhausen [3,4] studied, among many things, the function p(n). They were concerned with general conditions on sets, contained in {1,2,...,n}, that avoid the values of linear forms . Starting from a table of relevant coefficients in [3], Cassaigne proved a lower bound on the weakly triple-free set constant:



Here are more details. Direct computation of this constant requires extension of the table in [3], a time-consuming task. In a recent e-message, Graham told me that he, Erdös and others at AT&T estimated the constant to good accuracy in summer, 1996. A report of their work is expected soon.

Given fixed s>1, consider sets S of positive integers for which for all integers x. Denote the corresponding asymptotic maximal density by . What can be said about the asymptotics of as s approaches infinity? Spencer & Erdös [5] proved that there exist constants c and C for which



for all suitably large s, although specific numerical values were not presented.

Postscript I

Ronald Graham has kindly written the following:

I now have many results concerning the {x,2x,3x} and related problems.
The critical density for this set (i.e., the density of the smallest
subset of {1,2,...,n} which hits every subset of this form is
at most 0.1999914524 and at least 0.199039. If a reasonable geometrical
hypothesis holds, then I can show that this density is 0.19968056197...

It is interesting that for the related question of hitting all subsets
of the form (x,2x,3x,6x), the correct value of the critical density
is exactly 1/12. On the other hand, if you want to hit all the
real subsets of [0,1] with a set X, then X must have measure at
least 1/11 (and similarly, for the real case of {x,2x,3x} in [0,1],
X must have measure at least 1/5 = 0.200000... ).

All interested parties will watch for conference proceedings based on [6].

Postscript II

The awaited paper by Chung, Erdös & Graham [7] has now appeared, as well as my book [8].

Postscript III

Fix an integer r>1. Define a set S of positive integers to be r-fold-free if, for any integer x, the set .

Therefore a 2-fold-free set is the same as a double-free set, but a 3-fold-free set is not a triple-free set (in either sense). The maximum cardinality of r-fold-free sets was straightforwardly calculated by Reznick & Holzager [9]. A problem in [10] involves 3-fold-free sets. The asymptotic maximal density of 3-fold-free sets is 3/4 and, more generally [3], the asymptotic maximal density of r-fold-free sets is r/(r+1).

Various entries in Sloane's integer sequence database are directly relevant:

• A050292, the maximum cardinality of a double-free subset of {1,2,...,n}
• A157282, the maximum cardinality of a weakly triple-free subset of {1,2,...,n}
• A050296, the maximum cardinality of a strongly triple-free subset of {1,2,...,n}
• A050294, the maximum cardinality of a 3-fold-free subset of {1,2,...,n}

and

• A057561, the maximum cardinality of a weakly triple-free subset of {d(1),d(2),...,d(n)}
• A094708, the same as n-A057561(n), expressed in terms of "hitting" rather than "not encompassing"
• A157271, the maximum cardinality of a strongly triple-free subset of {d(1),d(2),...,d(n)}

where {d(1),d(2),...} is the set of all values of the form for nonnegative integers i and j, arranged in increasing order. Of secondary interest are:

• A050291, the number of double-free subsets of {1,2,...,n}
• A068060, the number of weakly triple-free subsets of {1,2,...,n}
• A050295, the number of strongly triple-free subsets of {1,2,...,n}
• A050293, the number of 3-fold-free subsets of {1,2,...,n}

and

• A157244, the weakly triple-free constant
• A157245, 1 - (the weakly triple-free constant)
• A086316, the strongly triple-free constant.

Acknowledgements

I am grateful to David Eppstein, Julien Cassaigne, Paul Zimmermann, Neil Calkin, Anusch Taraz and Ronald Graham for their valuable correspondence.

References

1. E. T. H. Wang, On double-free sets of integers, Ars Combinat. 28 (1989) 97-100; MR 91d:11011.
2. J. Cassaigne and P. Zimmermann, Numerical evaluation of the strongly triple-free constant, unpublished note (1996).
3. R. Graham, J. Spencer and H. Witsenhausen, On extremal density theorems for linear forms, Number Theory and Algebra, ed. H. Zassenhaus, Academic Press, 1977, pp. 103-109; MR 58 #569.
4. P. Erdös and R. Graham, Old and New Problems and Results in Combinatorial Number Theory, Enseignement Math. Monogr. 28, 1980, p. 20; MR 82j:10001.
5. J. Spencer and P. Erdös, A problem in covering progressions, Stud. Sci. Math. Hung. 30 (1995) 149-154; MR 96f:11018.
6. R. Graham, Extremal pattern-free sets of integers, and other favorite problems of Erdös, lecture abstract, Millennial Conference on Number Theory, May 2000, Univ. of Illinois at Urbana-Champaign.
7. F. Chung, P. Erdös, and R. Graham, On sparse sets hitting linear forms, Number Theory for the Millennium, v. 1, Proc. 2000 Urbana conf., ed. M. A. Bennett, B. C. Berndt, N. Boston, H. G. Diamond, A. J. Hildebrand, and W. Philipp, A. K. Peters, 2002, pp. 257-272; available online here; MR 2003k:11012.
8. S. R. Finch, Triple-free set constants, Mathematical Constants, Cambridge Univ. Press, 2003, pp. 183-185; MR 2004i:00001.
9. B. Reznick and R. Holzsager, r-fold free sets of positive integers, Math. Magazine 68 (1995) 71-72.
10. A. Engel, Problem-Solving Strategies, Springer-Verlag, 1998, p. 114; MR 98m:00004.

Copyright (c) 2002 Steven R. Finch.
All rights reserved.