 |
Non-Ideal Waring's Problem
Let N denote the set of all nonnegative integers.
A subset S of N is a basis of order h if every element of N
is a sum of exactly h elements of S (with repetitions allowed).
We write  .
Waring's problem involves the set .
Waring's problem involves the set 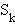 of all nonnegative kth powers of integers. Hilbert [14] proved that
of all nonnegative kth powers of integers. Hilbert [14] proved that
 for all suitably large h, for each k,
and the least possible h is called g(k). We discuss the calculation of
g(k) in our article Powers of 3/2 modulo one.
This is regarded as the "ideal" part of Waring's problem (even though it
is not yet completely solved). for all suitably large h, for each k,
and the least possible h is called g(k). We discuss the calculation of
g(k) in our article Powers of 3/2 modulo one.
This is regarded as the "ideal" part of Waring's problem (even though it
is not yet completely solved).
A subset S of N is an asymptotic basis of order h if every
sufficiently large element of N is a sum of exactly h elements of
S (again, with repetitions allowed). In the special case
 , define G(k) to be the least possible
h, for each k. Clearly , define G(k) to be the least possible
h, for each k. Clearly 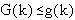 , and
Hurwitz [15] and Maillet [16] proved that , and
Hurwitz [15] and Maillet [16] proved that  .
In other words, there are arbitrarily large integers which are not the
sum of k kth powers [1]. .
In other words, there are arbitrarily large integers which are not the
sum of k kth powers [1].
We omit discussion [2,3] of a number of important estimates for
G(k), applicable for many values of k, and simply give the most current
results for small k-values:
| k |
who proved
and when |
lower
bound |
G(k) |
upper
bound |
who proved
and when |
| 2 |
Lagrange (1770) |
- |
4 |
- |
Lagrange (1770) |
| 3 |
Hurwitz & Maillet (1908) |
4 |
- |
7 |
Linnik (1943) |
| 4 |
Kempner (1912) |
- |
16 |
- |
Davenport (1939) |
| 5 |
Hurwitz & Maillet (1908) |
6 |
- |
17 |
Vaughan & Wooley (1995) |
| 6 |
Hardy & Littlewood (1922) |
9 |
- |
24 |
Vaughan & Wooley (1995) |
| 7 |
Hurwitz & Maillet (1908) |
8 |
- |
33 |
Vaughan & Wooley (1995) |
| 8 |
Hardy & Littlewood (1922) |
32 |
- |
42 |
Vaughan & Wooley (1995) |
| 9 |
Hardy & Littlewood (1922) |
13 |
- |
50 |
Vaughan & Wooley (1999) |
| 10 |
Hardy & Littlewood (1922) |
12 |
- |
59 |
Vaughan & Wooley (1999) |
| 11 |
Hurwitz & Maillet (1908) |
12 |
- |
67 |
Vaughan & Wooley (1999) |
| 12 |
Hardy & Littlewood (1922) |
16 |
- |
76 |
Vaughan & Wooley (1999) |
| 13 |
Hurwitz & Maillet (1908) |
14 |
- |
84 |
Vaughan & Wooley (1999) |
| 14 |
Hurwitz & Maillet (1908) |
15 |
- |
92 |
Vaughan & Wooley (1999) |
| 15 |
Hurwitz & Maillet (1908) |
16 |
- |
100 |
Vaughan & Wooley (1999) |
| 16 |
Hardy & Littlewood (1922) |
64 |
- |
109 |
Vaughan & Wooley (1999) |
| 17 |
Hurwitz & Maillet (1908) |
18 |
- |
117 |
Vaughan & Wooley (1999) |
| 18 |
Hardy & Littlewood (1922) |
27 |
- |
125 |
Vaughan & Wooley (1999) |
| 19 |
Hurwitz & Maillet (1908) |
20 |
- |
134 |
Vaughan & Wooley (1999) |
| 20 |
Hardy & Littlewood (1922) |
25 |
- |
142 |
Vaughan & Wooley (1999) |
| 21 |
Hardy & Littlewood (1922) |
24 |
- |
* |
* |
| 22 |
Hurwitz & Maillet (1908) |
23 |
- |
* |
* |
| 23 |
Hurwitz & Maillet (1908) |
24 |
- |
* |
* |
| 24 |
Hardy & Littlewood (1922) |
32 |
- |
* |
* |
| 25 |
Hurwitz & Maillet (1908) |
26 |
- |
* |
* |
| 26 |
Hurwitz & Maillet (1908) |
27 |
- |
* |
* |
| 27 |
Hardy & Littlewood (1922) |
40 |
- |
* |
* |
| 28 |
Hurwitz & Maillet (1908) |
29 |
- |
* |
* |
| 29 |
Hurwitz & Maillet (1908) |
30 |
- |
* |
* |
| 30 |
Hurwitz & Maillet (1908) |
31 |
- |
* |
* |
| 31 |
Hurwitz & Maillet (1908) |
32 |
- |
* |
* |
| 32 |
Hardy & Littlewood (1922) |
128 |
- |
* |
* |
The asterick (*) means that, while algorithms for computing bounds exist [5,7], I haven't
seen the bounds explicitly in print yet. The most recent reference [8] awaits publication.
See [9,10] for numerical evidence supporting the conjecture that
G(3)=4. Landreau [11] found a large integer 7373170279850 which requires more than four
cubes; conceivably this may be the largest such integer.
See also [12,13] for the asymptotics of the number of representations of n as a
sum of four cubes, which interestingly turns out to involve  ,
where ,
where  is Euler's gamma function. is Euler's gamma function.
Postscript
See [18] for recently gathered evidence that G(3)=4.
References
- G. H. Hardy and E. M. Wright, An Introduction to the Theory of
Numbers, 5th ed., Oxford 1985;
MR 81i:10002.
- P. Ribenboim, The Book of Prime Number Records, 2nd ed.,
Springer-Verlag, 1989;
MR 90g:11127.
- M. B. Nathanson, Additive Number Theory: The Classical Bases,
Springer-Verlag, 1996;
MR 97e:11004.
- R. C. Vaughan and T. D. Wooley, Further improvements in Waring's problem,
Acta Math. 174 (1995) 147-240;
MR 96j:11129a.
- T. D. Wooley, New estimates for smooth Weyl sums, J. London Math. Soc.
51 (1995) 1-13;
MR 96e:11109.
- Zai Zhao Meng, Some new results on Waring's problem, J. China Univ. Sci. Tech.
27 (1997) 1-5;
MR 98e:11115.
- T. D. Wooley, Large improvements in Waring's problem, Annals of Math. 135 (1992)
131-164;
MR 93b:11129.
- R. C. Vaughan and T. D. Wooley, Further improvements in Waring's problem,
IV: higher powers, Acta Arith. 94 (2000) 203-285.
- J. Bohman and C.-E. Fröberg, Numerical investigation of Waring's problem for cubes,
BIT 21 (1981) 118-122;
MR 82k:10063.
- F. Romani, Computations concerning Waring's problem for cubes, Calcolo
19 (1982) 415-431;
MR 85g:11088.
- D. Rusin, The Waring problem (Mathematical Atlas).
- J. Brüdern and N. Watt, On Waring's problem for four cubes, Duke Math. J.
77 (1995) 583-599;
MR 96e:11121.
- K. Kawada, On the sum of four cubes, Mathematika 43 (1996) 323-348;
MR 97m:11125.
- D. Hilbert, Beweis für die Darstellbarkeit der ganzen Zahlen durch eine feste
Anzahl nter Potenzen (Waringsches Problem), Nachrichten Königlichen
Gesellschaft der Wissenschaften zu Göttingen, Math.-Phys. Klasse (1909) 17-36;
Math. Annalen 67 (1909) 281-305.
- A. Hurwitz. Über die Darstellung der ganzen Zahlen als Summen von nter
Potenzen ganzer Zahlen, Math. Annalen 65 (1908) 424-427.
- E. Maillet, Sur la décomposition d'un entier en une somme de puissances
huitièmes d'entiers (Problème de Waring), Bull. Soc. Math. France
36 (1908) 69-77.
- W. J. Ellison, Waring's problem, Amer. Math. Monthly 78 (1971) 10-36;
MR 54 #2611.
- J.-M. Deshouillers, F. Hennecart and B. Landreau, 7,373,170,279,850, Math. Comp.
69 (2000) 421-439;
MR 2000i:11150.
Return to the Powers of 3/2 Modulo One essay.
Copyright © 1995-2001 by Steven Finch.
All rights reserved.
|
 .
Waring's problem involves the set
.
Waring's problem involves the set 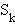 of all nonnegative kth powers of integers. Hilbert [14] proved that
of all nonnegative kth powers of integers. Hilbert [14] proved that
 for all suitably large h, for each k,
and the least possible h is called g(k). We discuss the calculation of
g(k) in our article Powers of 3/2 modulo one.
This is regarded as the "ideal" part of Waring's problem (even though it
is not yet completely solved).
for all suitably large h, for each k,
and the least possible h is called g(k). We discuss the calculation of
g(k) in our article Powers of 3/2 modulo one.
This is regarded as the "ideal" part of Waring's problem (even though it
is not yet completely solved).