Ulam s-Additive Sequences

Let s be a positive integer. A strictly increasing sequence of positive integers



is s-additive [1,2] if, for , is the least integer exceeding which has precisely s representations



The first terms of an s-additive sequence are called the base of the sequence. An s-additive sequence, for a given base, may be either finite or infinite; we assume the sequence is maximal in the sense that the total number of terms is as large as possible.

Here are three open problems (among many) associated with s-additive sequences. The first is well-known; the other two deserve more attention.

Consider the s-additive sequence with . The next fifteen terms of the sequence are

3, 4, 6, 8, 11, 13, 16, 18, 26, 28, 36, 38, 47, 48, 53

and more are given here. The sequence is infinite (as is any 1-additive sequence) since is an integer greater than with no other representation and, hence, there exists a least such integer. It is the archetypal s-additive sequence and was first studied by Ulam [3].

Open Problem: does Ulam's sequence have zero asymptotic density (relative to the positive integers)?

Consider the 1-additive sequence with and for some integer . It appears to be true that the only even terms in this sequence are



although a proof is not known. Computations show that the sequence for m=3 is regular in the sense that the sequence of sucessive differences



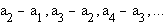
is eventually periodic. Moreover, when m=3, the smallest positive integer N such that



for all sufficiently large n is 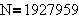. This integer N is called the period of the sequence. The fundamental difference of the sequence is likewise defined to be



for large enough n, and thus the asymptotic density of the sequence



is positive (in particular).

Open Problem: what are the values of N and D for the sequence for m=4?

Hint: use the fact that the number of even terms is (evidently) finite to build an efficient, low-memory algorithm for computing . Much more has been proved concerning the two (somewhat easier) cases:



and



References [1-7] should be consulted for details.

Consider the 2-additive sequence with . The next fifteen terms of the sequence are

5, 6, 8, 10, 12, 15, 17, 19, 29, 31, 33, 43, 44, 47, 51

and more are given here.

Open Problem: is this sequence infinite?

I suspect that the third problem is very hard, but the second problem should yield to some clever individual with enough computing power and patience to spare! Interested readers are urged to examine [1-7] as well as essays on the Stolarsky-Harborth constant and quadratic recurrence constants.

References

1. R. Queneau, Sur les suites s-additives, J. Combin. Theory Ser. A. 12 (1972) 31-71; MR 46 #1741.
2. S. Finch, Conjectures about 1-additive sequences, Fibonacci Quart. 29 (1991) 209-214; MR 92j:11009.
3. R. K. Guy, Unsolved Problems in Number Theory, 2nd ed., Springer-Verlag, 1994, section C4; MR 96e:11002.
4. S. Finch, On the regularity of certain 1-additive sequences, J. Combin. Theory Ser. A. 60 (1992) 123-130; MR 93c:11009.
5. S. Finch, Patterns in 1-additive sequences, Experim. Math. 1 (1992) 57-63; MR 93h:11014.
6. J. H. Schmerl and E. Spiegel, The regularity of some 1-additive sequences, J. Combin. Theory Ser. A. 66 (1994) 172-175; MR 95h:11010.
7. J. Cassaigne and S. Finch, A class of 1-additive sequences and quadratic recurrences, Experim. Math. 4 (1995) 49-60; MR 98c:11010.

Copyright © 1995-2001 by Steven Finch.
All rights reserved.