The Dimer Problem

Consider the 2n-by-2n planar square lattice L and call two vertices adjacent if the distance between them is 1. A dimer (or diatomic molecule) consists of two adjacent vertices of L and the (non-oriented) bond connecting them. A dimer covering of L is a collection of disjoint dimers whose union contains all the vertices of L. Here is an example of a dimer covering on the 4-by-4 lattice (n=2):



Kasteleyn [14], Fisher [15] and Temperley & Fisher [16] proved that, if f(n) denotes the number of distinct dimer coverings of L, then



They additionally proved that the so-called molecular freedom per dimer is



a fascinating and unexpected occurrence of Catalan's constant [14-29,45]. This is the solution, in graph theoretic terms, of the problem of counting perfect matchings on the square lattice. It is also the answer to the question: what is the number of ways of covering a 2n-by-2n chessboard with 2-by-1 or 1-by-2 dominoes? (See our essay on Kneser-Mahler polynomial constants for another appearance of the dimer constant.)

The three-dimensional analog of this problem remains one of the classical unresolved issues of solid-state chemistry.

A dimer arrangement is a collection of disjoint dimers (not necessarily a cover of L). Here is an example:



Let g(n) denote the number of distinct dimer arrangements, equivalently, the number of monomer-dimer coverings of L. An exact expression for the asymptotic result



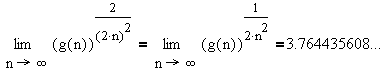
remains unknown.

Copyright © 1995-2001 by Steven Finch.
All rights reserved.