The OEIS is supported by the many generous donors to the OEIS Foundation.
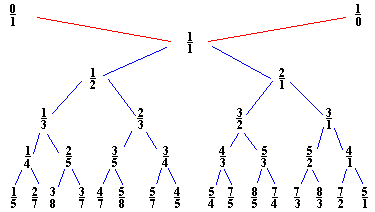
There are several versions of this tree. This one, which appears in R. L. Graham, D. E. Knuth and O. Patashnik, Concrete Mathematics. Addison-Wesley, Reading, MA, 1990, p. 117, was drawn by Alexander Bogomolny. For another version see J. C. Lagarias, Number Theory and Dynamical Systems, pp. 35-72 of S. A. Burr, ed., The Unreasonable Effectiveness of Number Theory, Proc. Sympos. Appl. Math., 46 (1992). Amer. Math. Soc.
The nth order Farey series is the set of reduced fractions between 0 and 1 whose denominators are n or less, arranged in increasing order, and corresponds to a subtree of the Stern-Brocot tree.
There are also many associated sequences: